Agenda
Sampling
Sample Size Estimation
Descriptive Statistics
Few FAQs
Sampling

Sampling is a process of selecting a subset of observations from a population to make inferences about various population parameters such as mean, proportion, standard deviation, etc.
Important: Sampling is necessary when it is difficult or expensive to collect data on the entire population. The incorrect sample may lead to incorrect inferences about the population
Note: Sampling error arises from estimating a population characteristic by looking at only one portion of the population rather than the entire population. It is equal to the difference between the estimate derived from a sample survey and the ‘true’ value that would result if a census of the whole population were taken under the same conditions. There is no sampling error in a census because the calculations are based on the entire population.
Sample Size Estimation
Measures such as Mean and Standard Deviation are calculated using the entire population and are also known as population parameters. These population parameters estimated from the sample are called sample statistics or statistics. Population proportion is the proportion of cases in the data belonging to a specific category, can also be calculated.
The sample size for analytics projects is determined using factors such as effect size, standard deviation, desired level of confidence and margin of error.

Numerical : A hospital wants to estimate the average time taken to discharge a patient after doctor clears them. Calculate the required sample size at a confidence of 95% and Maximum error in estimation of 5 mins, assuming the SD is 30 mins
Step 1 : Calculation of Z value
Area under the curve Aₗ = CL/2
Aₗ=0.95/2
Aₗ = 0.475
check Z score for this area in table which comes out to be = 1.9+0.06 = 1.96
Step 2 : Calculation of Sample Size putting Z = 1.96, S.D = 30, ME = 5 in the above formula n =138.2976
Therefore Sample size of 138 is to be selected.
Descriptive Statistics
Descriptive statistics is about finding “what has happened” by summarizing the data using innovative methods and analyzing the past data.
Commonly used methods for this are:
Measures of Central Tendency
Measures of Dispersion (or Variability)
Measures of Shape
Measures of Central Tendency
These are the measures that are used for describing the data using a single value.
They include — Mean, Median and Mode
Mean — If the entire population is available and if we calculate mean based on the entire population, then we get the population mean. Among the measures of central tendency, mean is the most frequently used measure since it uses all the observations (all Xi values) in the data set (either sample or population) to calculate the mean value. Be careful as Mean is significantly affected with the presence of outliers.

Median — It is the value that divides the data into two equal parts. It is calculated by first arranging the data in increasing order.
If the number of observations are odd, then median is given by the middle observation in the sorted order. That is, the value at position (n + 1)/2 when n is odd
If the number of observations are even, median is given by the mean of the two middle observation in the sorted order. That is median is the average value of (n/2)th and (n + 2)/2 th observation
Median is much more stable than the mean value, that is adding a new observation may not change the median significantly. However, the drawback of median is that it is not calculated using the entire data like in the case of mean.
Mode — It is the most frequently occurring value in the data set. It is the only measure of Central Tendency which is valid for qualitative (nominal) data since the mean and median for nominal data are meaningless. If each value in the data set appears only once, then there is no mode in the data set.
If the distribution is symmetrical, Mean = Median = Mode.
Eg — Normal Distribution
Joke of the article : If someone’s head is in freezer and leg is in the oven, the average body temperature would be fine, but the person may not be alive.
Measures of Dispersion (or Variability)
Variability in the data is measured using the following measures:
Range
Inter-Quartile Distance (IQD)
Variance
Standard Deviation
Range — Range is the difference between maximum and minimum value of the data. It captures the data spread.
Inter-Quartile Distance — Inter-quartile distance (IQD), also called inter-quartile range (IQR), is a measure of the distance between Quartile 1 (Q1) and Quartile 3 (Q3).
Outliers — are an observation which is far away (on either side) from the mean value of the data. Values of data below Q1–1.5 IQD and above Q3 + 1.5 IQD are classified as outliers.
Variance — It is a measure of variability in the data from the mean value.

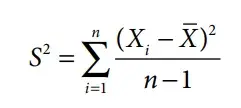
Standard Deviation — The square root of Variance is called Standard Deviation and is calculated as


Measures of Shape
These are
Skewness
Kurtosis
Skewness — It is a measure of symmetry or lack of symmetry.
A data set is symmetrical when the proportion of data at equal distance (measured in terms of standard deviation) from mean (or median) is equal.
There are many different approaches to measuring skewness. Pearson’s moment coefficient of skewness for a data set with n observations is given by

The value of g1 will be close to 0 when the data is symmetrical. A positive value of g1 indicates a positive skewness and a negative value indicates negative skewness.


Kurtosis — It is another measure of shape, aimed at shape of the tail, that is, whether the tail of the data distribution is heavy or light. Kurtosis is measured using the following equation:
There are three kinds of Kurtosis:
Mesokurtic —when the kurtosis is zero, similar to the normal distributions. (Kurtosis value=3)
Leptokurtic — when the tail of the distribution is heavy (outlier present) and kurtosis is higher than that of the normal distribution. (Kurtosis value>3)
Platykurtic — when the tail of the distribution is light( no outlier) and kurtosis is lesser than that of the normal distribution. (Kurtosis value<3)

Few FAQs
Estimated value of parameter from a sample is called → Sample Statistic
Central limit theorem for sampling distribution is valid only when → Large samples drawn from any independent and identically distributed population ( when number of data points is at least 30)
Which relation is correct for a negative skewed distribution? →
Mean<Median<Mode
Presence of Outliers in a dataset not affects which— Mean, IQR,SD or Range → IQR as it is essentially the range of the middle 50% of the data. Since it uses the middle 50%, therefore it is not affected by the outliers.
Understanding the basic Statistical concepts for an Analyst who is just starting out is an added advantage. This blog will help in understanding the concepts easily for the beginners as well as act as a refresher for already learned. For more resources and/or any guidance for transitioning into Data Science, connect with us on LinkedIN

Comments